参考资料：

• GAMES101_Lecture_03_Transformation Cont
• GAMES101-现代计算机图形学入门-闫令琪

在介绍三维空间的变换前，先来了解一个概念：正交矩阵

我们知道，在二维空间中，对图形 $G$$G$​​ 旋转 $\theta$$\theta$​​ 角度得到图形 $G^{\prime }$$G^\prime$​​，可以用矩阵表示该旋转操作为：

那么，图形 $G^{\prime }$$G^\prime$ 旋转 $-\theta$$-\theta$ 角度得到原图形 $G$$G$，用矩阵表示该操作为：

我们知道：

从而可以得到：

对比 $R_{\theta }$$R_\theta$​ 与 $R_{-\theta }$$R_{-\theta}$​，不难发现 $R_{-\theta }$$R_{-\theta}$​ 等于 $R_{\theta }$$R_{\theta}$​ 的转置矩阵，即：

同时， $R_{\theta }$$R_\theta$ 与 $R_{-\theta }$$R_{-\theta}$​ 互为逆变换，那么根据逆变换的定义，可以得到：

最终可得：

如果一个矩阵的转置矩阵和逆矩阵相同，那么我们称这个矩阵为正交矩阵。不仅在二维空间中旋转操作为正交矩阵，在三维矩阵中同样如此。

在《齐次坐标》中，我们知道齐次坐标同样可用在三维空间中：

• 三维中的点 ：$(x,y,z,1{)}^T$$(x,\ y,\ z,\ 1)^T$
• 三维中的向量：$(x,y,z,0{)}^T$$(x,\ y,\ z,\ 0)^T$

通常，任意 $(x,y,z,w)$$(x,\ y,\ z,\ w)$，当 $w\ne 0$$w \neq 0$ 时，都可以表示三维空间中的一个点：$(x/w,y/w,z/w)$$(x/w,\ y/w,\ z/w)$

1 缩放

2 旋转

在三维空间中，旋转可能是沿任意方向的旋转，在这之前，先看一下比较简单的沿 $x$$x$、$y$$y$ 或者 $z$$z$ 轴单一方向的旋转。

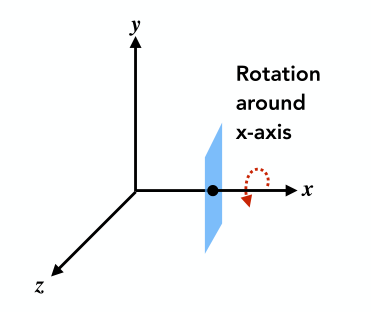
上图表示为沿 $x$$x$ 轴方向旋转一定的角度 $\alpha$$\alpha$​，不难写出该旋转的矩阵表示：

同样，我们可以写出沿 $z$$z$ 轴旋转的矩阵表示为：

沿 $y$$y$ 轴旋转的矩阵表示为：

在沿 $y$$y$​ 轴旋转的矩阵表示中，情况与前2者稍有不同，$sin(\alpha )$$sin(\alpha)$​ 的正负发生了变化，这是因为根据右手定则，$\overrightarrow{x}\times \overrightarrow{y}=\overrightarrow{z}$$\vec{x}\times\vec{y} = \vec{z}$​、$\overrightarrow{y}\times \overrightarrow{z}=\overrightarrow{x}$$\vec{y}\times\vec{z} = \vec{x}$​，但是 $\overrightarrow{x}\times \overrightarrow{z}=-\overrightarrow{y}$$\vec{x}\times\vec{z} = -\vec{y}$​​ ，所以正负号发生了变化。​

在二维空间变换中，沿任意方向旋转，我们可以将该方向向量的起点平移至原点，然后做旋转操作，最后再将该方向向量的原点平移回原位置。

同样，在三维空间中，沿任意方向旋转，我们同样可以先将该方向向量的起点平移至原点，然后做旋转，最后再平移回去。三维空间中的任意向量都可以分解成由 $x$$x$、$y$$y$、$z$$z$ 轴的投影组成，如果能够将任意方向的旋转也能分解成沿 $x$$x$、$y$$y$、$z$$z$ 轴，那么沿任意方向的旋转问题便可以分解成更加简单的组合，这该有多好。

那么沿任意方向的旋转是否能够分解成沿 $x$$x$、$y$$y$、$z$$z$ 轴的旋转组合呢？或者说，三维空间中的任意方向，能够通过沿 $x$$x$、$y$$y$、$z$$z$​ 轴的旋转得到呢？

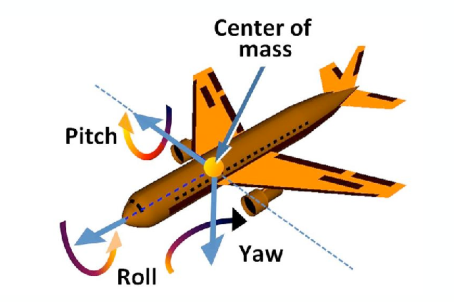
答案是可以的，我们可以想象飞机的中心为原点，分级通过沿 $x$$x$（上下“点头”）、$y$$y$（左右“摇头”）、$z$$z$（侧向“翻转”） 轴方向的旋转实现机头朝向任意方向，那么三维空间中沿任意方向的旋转可以分解成 $x$$x$、$y$$y$、$z$$z$​ 轴的旋转组合：

在三维空间中，沿任意轴 $nn$$\pmb{n}$ 旋转 $\alpha$$\alpha$ 角度，有人给出了其对应的旋转公式，即 罗德里格斯旋转公式（Rodrigues’ Rotation Formula）：

点击此处 可查看该公式的推导。

3 平移

4 仿射