参考资料:
1 线性变换
在二维平面中,图形变换后坐标满足以下关系:
同时,该关系可以表示为矩阵形式:
那么,我们称这种变化为线性变换。
线性变换包括缩放、反射、切变、旋转。
1.1 缩放
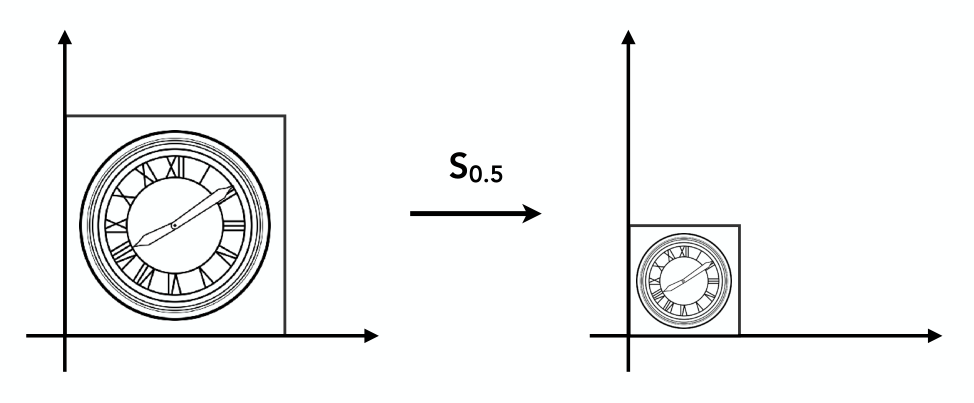
上图表示将左侧图形沿着x和y方向缩放相同的0.5倍(称之为均匀缩放),那么缩放后的坐标与原坐标关系为:
我们可以用矩阵来表示这个关系:
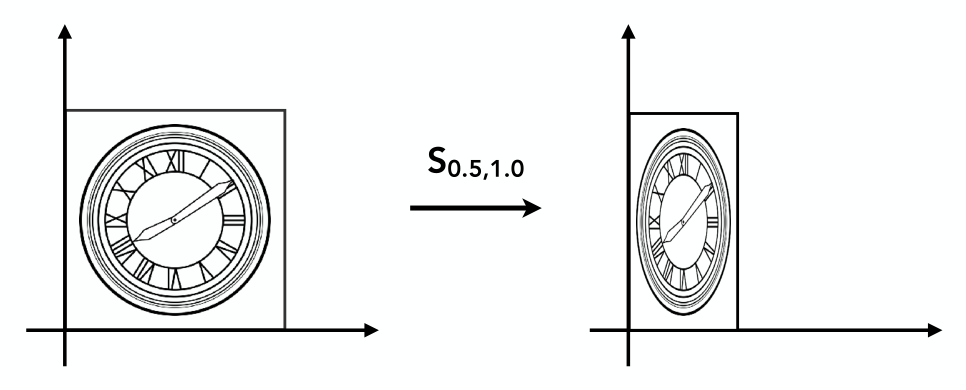
上图表示将左侧图形沿着x和y方向分别缩放0.5倍和1被(称之为非均匀缩放),那么缩放后的坐标与原坐标关系为:
我们可以用矩阵来表示这个关系:
综上两个示例,可以得到在二维平面中,如果沿着x和y方向分别缩放
用矩阵表示为:
1.2 反射(对称)
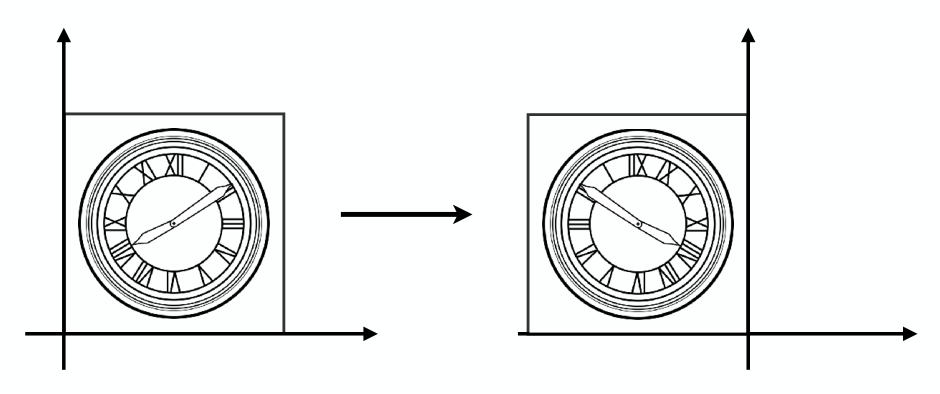
上图表示将左侧图形以y方向做对称操作,那么对称后的坐标与原坐标关系为:
可以用矩阵来表示为:
1.3 切变
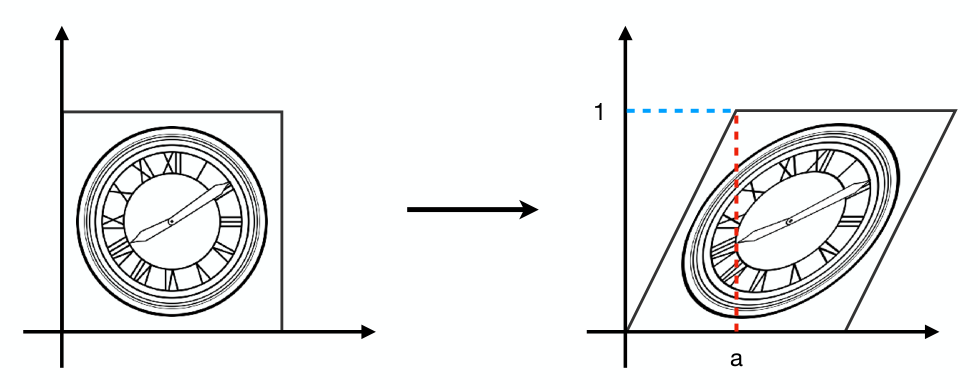
上图表示将左侧图形底部固定,沿着x方向拉伸右上角的点,使其移动a个单位(称之为切变),那么切变后的坐标与原坐标关系为:
可以用矩阵来表示为:
1.4 旋转
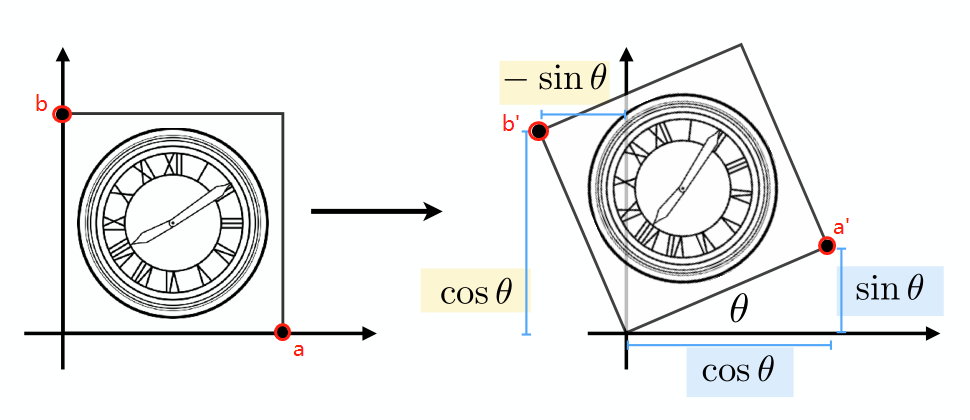
上图表示将左侧以原点为中心,逆时针旋转
我们将
根据矩阵乘法,得到
即
同理,将
从而得到旋转变换的矩阵表示为:
2 平移变换
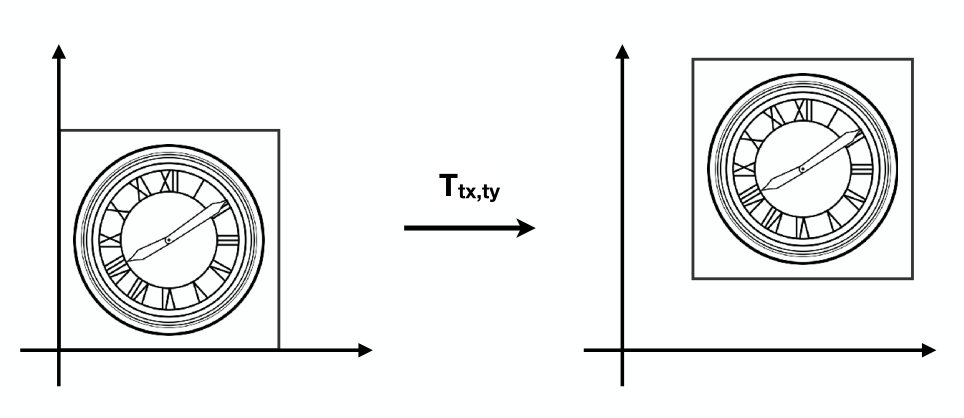 上图表示将左侧图形沿
上图表示将左侧图形沿
而通过了解《齐次坐标》,我们知道可以用如下矩阵形式表示:
3 逆变换
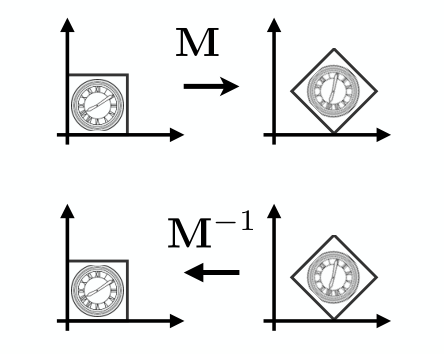
上图表示左上角图形经过
4 仿射变换
仿射变换由一次线性变换和一次平移变换组成,用矩阵形式表示为:
引入齐次坐标后矩阵表示为:
5 组合变换
在二维空间中,任何复杂的变换都可以分解成一个个的线性变换或者平移变换,以下图为例:
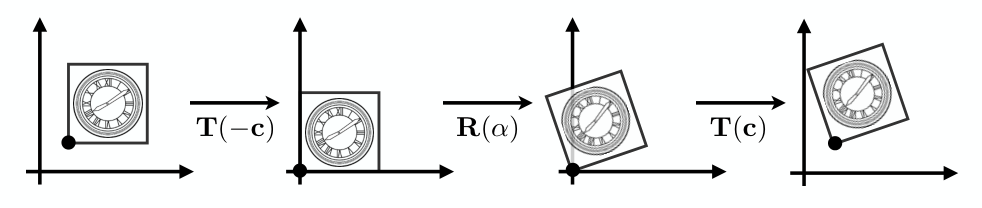
将最左侧图形以图中标记的点为中心,逆时针旋转一定的角度得到最右侧图形,理解起来很简单,但是纵观上文中讲解的所有变换,发现其不属于任何一种,我们可以称之为一个复杂变换。
对于复杂变换,我们可以将其分解为多个简单变换的组合:最左侧图形先做平移变换
用矩阵表示为:
注意,矩阵相乘的顺序为从右到左,对应变换操作的从前到后,由于矩阵相乘不满足交换律,所以矩阵的左右位置是固定不可变的,除非变换操作的顺序发生变化。